
ADEMÁS:
Gracias a Pedro Miguel González Urbaneja (por su interesante aportación)
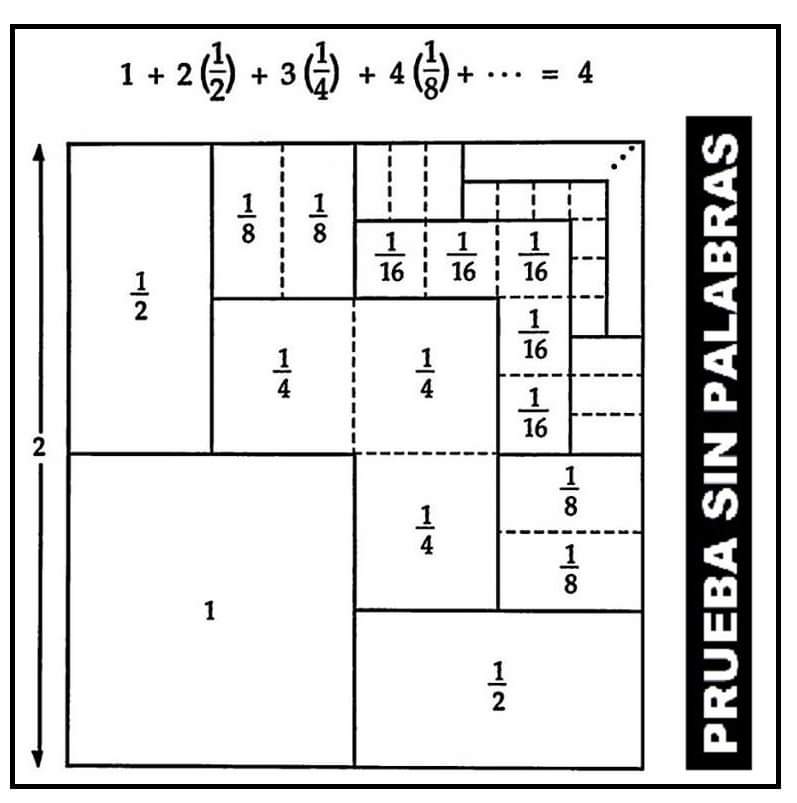
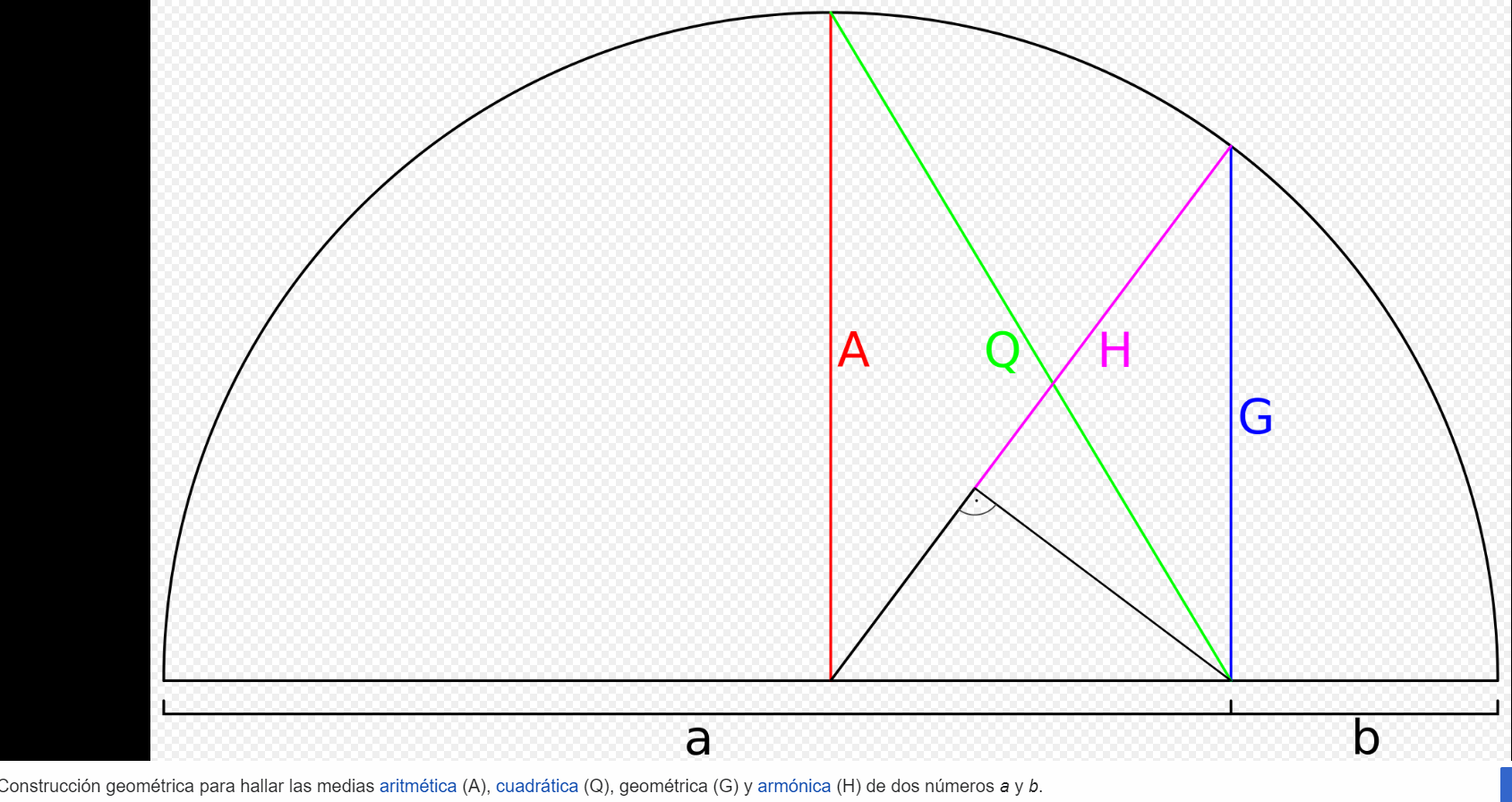
Normalmente cuando hablamos de media de dos números nos referimos a la media aritmética, es decir, a la mitad de su suma. Pero ¿sabias que existen otras medias de dos números dados?
Media aritmética —> Media aritmética – Wikipedia, la enciclopedia libre
Media geométrica —> Media geométrica – Wikipedia, la enciclopedia libre
Media cuadrática —> Media cuadrática – Wikipedia, la enciclopedia libre
Media armónica —> Media armónica – Wikipedia, la enciclopedia libre
Debe estar conectado para enviar un comentario.