Recomiendo verlos en YouTube y suscribirse a dicho canal.
Category / General
Libreoffice Math (ver. 7)
Canal de Youtube de las calculadoras Casio Classwiz
Suscríbete al canal de YouTube de Casio Classwiz para aprender el uso de esta estupenda y nueva calculadora.
Algunas identidades notables
Teorema de Bayes
Gracias a Superprof.es
Polígono equilátero no regular
Feliz 2024
2024 es divisible entre 8 (cubo perfecto); además 2024 se puede descomponer como suma de 8 cubos consecutivos: 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3.
Lotería de Navidad (segunda parte)
Lotería de Navidad (primera parte)
Nuevas calculadoras Casio
Calendario científico escolar 2023
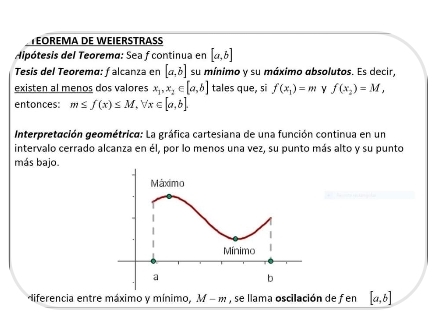
Teorema de Weiertrass
El sistema D´hont
Solución al problema de «María, Elena y Ana»
La ciencia detrás de la magia
Famosos que nacieron un 28 de abril (fíjate en el que aparece en la última fila, a la derecha)
profe.mates.jac 
Debe estar conectado para enviar un comentario.